Least-Cost Rule
The Resource Costs Cheat Sheet is here.
Least Cost Rule: production at least cost requires the ratio of labor’s marginal product to its price equals the ratio of capital’s marginal product to its price. The amounts of labor and capital employed must be adjusted, all the while keeping output constant, until this condition is achieved.
Simple, yes. (NO) The least cost rule comes into affect when the college board asks us to evaluate two inputs for production. Labor and Capital,,, workers and machines.
We are usually given two inputs, (labor and capital) and asked to evaluate which we need to buy more.
First - Let's create our own simple problem.
The price of labor is $10 and the price (rent) on capital is $20. The marginal product of labor is 40 and the marginal product of capital is 60. Should we hire more labor or more capital?
Remember the formula:
Set up the numbers:
What does this mean:
The marginal product of the last input of labor was 40 units produced and that labourer was paid $10. So for each $1 spent we received 4 units produced. 40/10 = 4
&
The marginal product of the last input of capital was 60 units produced and the rent was $20. So for each $1 spent we received 3 units produced. 60/20 = 3
Answer - Obviously we would want to hire more labor as (per dollar spent) on labourers produce a higher level of output. We want the biggest bang for the buck.
This is the simplest most straight forward way of presenting these problems don't expect it.
Answer - (A) The marginal product per dollar spent on labor is equal to the marginal product per dollar spent on capital.
2000 AP Multiple Choice Question
To answer this question you must understand that the Profit Max rule is about setting the ratios equal to one. There is a point where the right combination of labor and capital is maximised, this is always at the profit max (MR=MC) point on our graphs. If we are at Profit Max then the least cost rule is attained/satisfied.
Lets plug in some numbers: for answer (A)
This combination of capital and labor we would want to hire more labor.
Lets plug in the numbers for (E)
Answer (E) Both sides (ratios) equal each other. We are at profit max = least cost combination.
2008 AP Multiple Choice Question
Formula:
or
OK, so we can see clearly that we would want to hire more (increase) labor as the output per dollar is greater for labor. But, the confusion is should we choose answer (D) or (E).
The marginal product of the last input of labor was 40 units produced and that labourer was paid $10. So for each $1 spent we received 4 units produced. 40/10 = 4
If we increase the amount of labor we hire the MP will fall due to diminishing marginal returns.
&
The marginal product of the last input of capital was 60 units produced and the rent was $20. So for each $1 spent we received 3 units produced. 60/20 = 3
If we decrease the amount of capital we hire the MP will rise due to increasing marginal returns.
Remember, it is the least-cost rule, we want the least inputs we can hire(rent) to get to profit max.
Answer - (E) Increase labor and decrease capital.
(Practise Problem)
Answer (A) make no changes as the mix of inputs (last dollar spent yield the same marginal product)
(Practise Problem)
Answer (D) less labor and more capital.
(FRQ Practise)
then...
or
(10,000/1,000) = (50/w)
(W = 5)









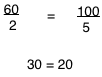



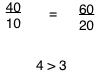












Thank you
ReplyDeleteThanks!
ReplyDeleteGreat help, thanks so much!
ReplyDeleteFound this very helpful thanks a lot
ReplyDeleteYou are very welcome,, Good Luck
ReplyDeleteOn the first question, you mentioned that we should hire more labor because it leads to higher level of output; however, you also mentioned that hiring more labor would decrease efficiency due to law of diminishing marginal returns. Then in the end why do we still increase labor? Also, I thought that in order to reach max efficiency, the ratios need to be the same; then shouldn't we increase capital?
ReplyDeleteOn the first question the understanding is that a $1 spent on labor provides 4 units produces while $1 spent on capital only provides 3 units produced. We want to spend our money on what gives us the most output per dollar spent - - Now where did I say that hiring more labor would decrease efficiency??? I did say,, ((If we increase the amount of labor we hire the MP will fall due to diminishing marginal returns. )) This holds true in that we want more of labor as they are the most efficient and less capital as it is less efficient,, decrease the amount of capital hired and the MP will increase and therefore the ratios of labor to capital will equalize much quicker. If you increased capital the MP of capital would fall and you would get less output per dollar spent. That wouldn't be right...
ReplyDeleteI have an exam tomorrow in AP Econ and I found this super helpful! Thank you so much!
ReplyDeleteThis is excellent explanation. Thanks
ReplyDelete